[LeetCode] 105. Construct Binary Tree from Preorder and Inorder Traversal

Problem

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

Example 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

Constraints:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder and inorder consist of unique values.
• Each value of inorder also appears in preorder.
• preorder is guaranteed to be the preorder traversal of the tree.
• inorder is guaranteed to be the inorder traversal of the tree.

---

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return helper(0, 0, inorder.length - 1, preorder, inorder);
    }
    public TreeNode helper(int preRoot, int inLeft, int inRight, int[] preorder, int[] inorder) {
        if (preRoot > preorder.length - 1 || inLeft > inRight)
            return null;
        TreeNode root = new TreeNode(preorder[preRoot]);
        int inRoot = 0;
        for (int i = inLeft; i <= inRight; i++)
            if (inorder[i] == root.val)
                inRoot = i;
        root.left = helper(preRoot + 1, inLeft, inRoot - 1, preorder, inorder);
        root.right = helper(preRoot + inRoot - inLeft + 1, inRoot + 1, inRight, preorder, inorder);
        return root;
    }
}

Explanation

• 배열 preorder의 첫 번째 요소가 Root노드가 된다. 그리고 이진 트리의 각 노드들은 unique한 값을 가지고 있기 때문에, 배열 preorder에서 찾은 Root노드의 값으로 배열 inorder에서도 Root노드를 찾을 수 있다.
• 배열 inorder에서 Root노드의 값를 찾았으니, 해당 값 좌측의 요소들이 Root노드의 좌측 자식 노드가 되고, 우측의 요소들이 Root노드의 우측 자식 노드가 된다.
• 예시 1의 경우 다음과 같이 나타낼 수 있다.

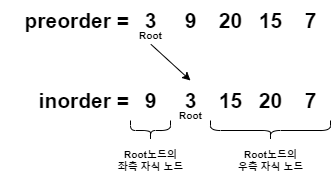
• 배열 inorder에서 Root노드의 좌측과 우측 자식 노드를 찾았기 때문에 이 노드들을 배열 preorder에서도 찾을 수 있다.

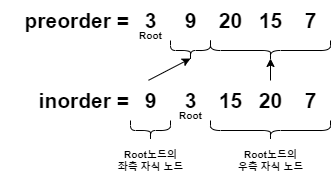
• 좌우측 자식 노드 중 자식 노드가 하나만 있다면 해당 노드를 Root노드의 자식 노드로 달아주면되고, 자식 노드가 여러개 있다면 이진 트리를 형성한다는 의미가 되고, 이 이진 트리의 Root노드를 기존의 Root노드에 달아주면 된다.
• 자식 이진 트리가 존재하는 경우에는 크기가 더 작은 배열 preorder와 inorder이 존재하는 경우와 같으므로 위와 같은 과정을 반복하면 되므로 설명은 생략한다.

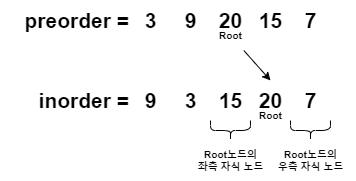
• Root노드의 자식 노드를 달아주려면 좌우측 자식 이진 트리에서 Root노드를 반환해주는 반복을 수행해야 한다. 본 문제에서는 재귀 함수를 선언하여 해결하도록 한다.
• 재귀 함수를 호출함에따라 사용하는 배열 preorder의 크기가 달라지기 때문에 배열 preorder속 Root노드의 값을 가리키는 변수 preRoot를 재귀 함수의 선언부에 작성한다.
• Root노드를 반환하기 위해 배열 preorder의 첫 요소를 변수 root에 할당하고 변수 root를 반환한다.

  public TreeNode helper(int preRoot, int[]preorder) {
    TreeNode root = new TreeNode(preorder[preRoot]);
    return root;
  }
  

• 다음으로 배열 inorder속 Root노드의 값을 알아야 배열 preorder속 요소들을 좌측과 우측 자식 노드로 나눌 수 있다.
• 배열 inorder속 Root노드의 값을 가르키는 인덱스를 나타내기 위해 변수 inRoot를 선언한다.
• for반복문을 작성해 배열 inorder속 Root노드의 값을 찾는다. 이 때 재귀 함수를 반복 호출 하면서 배열 inorder의 길이도 달라지고, for반복문 안에서 배열 inorder의 시작과 끝이 필요하기 때문에 배열 inorder의 시작과 끝을 나타내는 변수 inLeft와 inRight를 재귀 함수 선언부에 작성하고 for반복문에 이용한다.

  public TreeNode helper(int preRoot, int inLeft, int inRight, int[]preorder, int[] inorder) {
    TreeNode root = new TreeNode(preorder[preRoot]);
    int inRoot = 0;
    for (int i = inLeft; i <= inRight; i++)
        if (inorder[i] == root.val)
            inRoot = i;
    return root;
    }
  

• 재귀 함수를 호출하여 Root노드의 좌측과 우측 자식 노드를 달아준다. 그리고 재귀 함수 반복 호출 중 재귀 함수의 호출을 멈출 수 있도록 if조건문을 작성한다.

  public TreeNode helper(int preRoot, int inLeft, int inRight, int[]preorder, int[] inorder) {
    // 재귀 함수 호출 중단(null 반환)
    if (preRoot > preorder.length - 1 || inLeft > inRight)
        return null;
    TreeNode root = new TreeNode(preorder[preRoot]);
    int inRoot = 0;
    for (int i = inLeft; i <= inRight; i++)
        if (inorder[i] == root.val)
            inRoot = i;
    root.left = helper(preRoot + 1, inLeft, inRoot - 1, preorder, inorder);
    root.right = helper(preRoot + inRoot - inLeft + 1, inRoot + 1, inRight, preorder, inorder);
    return root;
    }
  

• 함수에서 재귀함수가 반환하는 값을 반환하도록 한다.

  return helper(0, 0, inorder.length - 1, preorder, inorder);