[LeetCode] 108. Convert Sorted Array to Binary Search Tree

Problem

Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.

A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.

Example 1:

Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted:

Example 2:

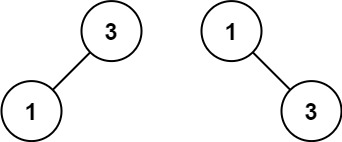
Input: nums = [1,3]
Output: [3,1]
Explanation: [1,null,3] and [3,1] are both height-balanced BSTs.

Constraints:

• 1 <= nums.length <= 10^4
• -10^4 <= nums[i] <= 10^4
• nums is sorted in a strictly increasing order.

Solution

Logic

1. 배열의 중앙에 위치하는 요소가 배열의 Root 노드의 값이 되므로 전체 배열에서 중앙에 위치하는 요소를 Root 노드의 값으로 만든다.

2. 배열 내에서 Root 노드의 값에 해당하는 요소의 좌측 배열과 우측 배열 각각 중앙에 위치한 요소가 Root 노드의 좌측, 우측 자식 노드의 값이 된다.

3. 위 과정을 반복하되, 배열의 범위를 벗어나는 요소를 참조하려 하거나 이미 참조한 요소를 다시 참조하려는 경우 반복을 중단한다.

   Code

   /**
    * Definition for a binary tree node.
    * public class TreeNode {
    *     int val;
    *     TreeNode left;
    *     TreeNode right;
    *     TreeNode() {}
    *     TreeNode(int val) { this.val = val; }
    *     TreeNode(int val, TreeNode left, TreeNode right) {
    *         this.val = val;
    *         this.left = left;
    *         this.right = right;
    *     }
    * }
    */
   class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        TreeNode root = buildTree(nums, 0, nums.length - 1);
        return root;
    }
    private TreeNode buildTree(int[] nums, int left, int right) { // left, right는 배열 속 인덱스
        if (right < left) return null; // right < left 일 때 배열의 범위를 벗어난 요소를 참조하거나 참조했던 요소를 다시 참조하는 꼴
        int center = (left + right) / 2;
        TreeNode node = new TreeNode(nums[center]);
        node.left = buildTree(nums, left, center - 1);
        node.right = buildTree(nums, center + 1, right);
        return node;
    }
   }
   

   Time Compexity