[LeetCode] 160. Intersection of Two Linked Lists

Problem

Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.

For example, the following two linked lists begin to intersect at node c1:

The test cases are generated such that there are no cycles anywhere in the entire linked structure.

Note that the linked lists must retain their original structure after the function returns.

Custom Judge:

The inputs to the judge are given as follows (your program is not given these inputs):

• intersectVal - The value of the node where the intersection occurs. This is 0 if there is no intersected node.
• listA - The first linked list.
• listB - The second linked list.
• skipA - The number of nodes to skip ahead in listA (starting from the head) to get to the intersected node.
• skipB - The number of nodes to skip ahead in listB (starting from the head) to get to the intersected node. The judge will then create the linked structure based on these inputs and pass the two heads, headA and headB to your program. If you correctly return the intersected node, then your solution will be accepted.

Example 1:

Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,6,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.

Example 2:

Input: intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Intersected at '2'
Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect).
From the head of A, it reads as [1,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.

Example 3:

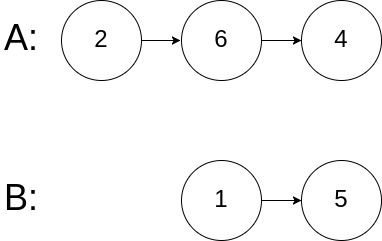
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: No intersection
Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.

Constraints:

• The number of nodes of listA is in the m.
• The number of nodes of listB is in the n.
• 1 <= m, n <= 3 * 10^4
• 1 <= Node.val <= 10^5
• 0 <= skipA < m
• 0 <= skipB < n
• intersectVal is 0 if listA and listB do not intersect.
• intersectVal == listA[skipA] == listB[skipB] if listA and listB intersect.

Follow up: Could you write a solution that runs in O(m + n) time and use only O(1) memory?

Solution

Logic

1. 두 연결 리스트의 길이를 각각 구한다.

2. 두 연결 리스트 길이의 차이를 구하고 길이가 더 긴 연결 리스트의 포인터를 해당 차이만큼 다음 노드를 참조하도록 한다.

3. 두 연결 리스트 각각의 포인터들이 참조하고 있는 노드가 같다면 해당 노드를 반환하고, 그렇지 않다면 두 연결 리스트 각각의 포인터가 다음 노드를 참조하도록 한다.

4. 끝까지 포인터를 변경하여 노드를 참조했음에도 같은 노드가 발견되지 않으면 null을 반환한다.

   Code

   /**
    * Definition for singly-linked list.
    * public class ListNode {
    *     int val;
    *     ListNode next;
    *     ListNode(int x) {
    *         val = x;
    *         next = null;
    *     }
    * }
    */
   public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode curA = headA, curB = headB;
        int m = 0, n = 0;
        while (curA != null || curB != null) {
            if (curA != null) {
                curA = curA.next;
                m++;
            } if (curB != null) {
                curB = curB.next;
                n++;
            }
        }
        for (int i = 0; i < Math.abs(n - m); i++) {
            if (m < n) headB = headB.next;
            else headA = headA.next;
        }
        while (headA != null && headB != null) {
            if (headA == headB) return headA;
            headA = headA.next;
            headB = headB.next;
        } return null;
    }
   }
   

   Time Complexity

   • 연결 리스트 A의 길이를 m, B의 길이를 n이라 가정할 때, 코드의 수행 시간을 좌우하는 것은 첫 번째 while반복문의 Max(m, n) 계산 횟수이다. 따라서 본 솔루션은 O(m), O(n)중 큰 값의 시간 복잡도를 가진다.