[LeetCode] 98. Validate Binary Search Tree

Problem

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

Input: root = [2,1,3]
Output: true

Example 2:

Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Constraints:

• The number of nodes in the tree is in the range [1, 10^4].
• -2^31 <= Node.val <= 2^31 - 1

---

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        Stack<TreeNode> stack = new Stack<TreeNode>();
        TreeNode prev = null;
        while (root != null || stack.isEmpty() == false) {
            while (root != null) {
            stack.push(root);
            root = root.left;
            }
            root = stack.pop();
            if (prev != null && root.val <= prev.val)
                return false;
            prev = root;
            root = root.right;
        }
        return true;
    }
}

Explanation

• 다음과 같은 트리가 있다고 가정하자.

• 위 트리가 BST(이진 검색 트리)인지 확인하기 위해서는 아래의 순서로 대소 비교를 수행해야 한다.

순서 \ 비교노드	노드 1	노드 2
1.	1번 노드	2번 노드
2.	2번 노드	3번 노드
3.	3번 노드	4번 노드
4.	4번 노드	5번 노드
5.	5번 노드	6번 노드
6.	6번 노드	7번 노드

• 노드간 비교를 수행해야 할텐데, 이를 위해서는 노드가 2개 필요하다. 하나는 root 노드를 활용하면 될 것이고, 다른 하나를 위해 prev 노드를 선언한다.
• 그리고 비교를 진행하기 위해서 트리의 아래쪽으로 내려가야 하는데, 이 때, 왔던 길을 돌아가기 위해서, 직전에 방문했던 노드를 꺼내 쓸 수 있는 자료구조 Stack을 선언한다.

  Stack<TreeNode> stack = new Stack<TreeNode>();
  TreeNode prev = null;
  

• 1번 비교를 수행하기 위해 root 노드를 좌측 최하단 자식노드로 보내기 위한 while 반복문을 작성한다.

  while (root != null) {
  stack.push(root);
  root = root.left;
  }
  root = stack.pop();
  

• 위의 while 반복문은 root 노드를 Stack에 담는 기능만 하므로, 또 다른 while 반복문으로 감싸서 노드간 비교를 진행할 수 있도록 한다.
• root 노드가 null 이거나 Stack이 비었다는 것은 노드간 비교를 문제없이 마쳤고, 해당 트리가 BST(이진 검색 트리)에 해당한다는 의미이므로, while 반복문을 빠져나가도록 한다.

  while (root != null || stack.isEmpty() == false) {
    while (root != null) {
    stack.push(root);
    root = root.left;
    }
    root = stack.pop();
    if (prev != null && root.val <= prev.val)
        return false;
    prev = root;
    root = root.right;
  }
  

• root 노드가 Stack에 담기면서 내려왔기 때문에, 직전에 방문했던 노드로 돌아갈 수 있다. 위의 표를 참고하여, root 노드가 노드를 이동하면서 2번 노드가 되고, prev 노드가 1번 노드가 되도록 한다.

  if (prev != null && root.val <= prev.val)
    return false;
  prev = root;
  root = root.right;
  

• 위의 if 조건문직전 까지를 1회전이라 하면 회전되는 동안의 과정은 다음 그림과 같다.

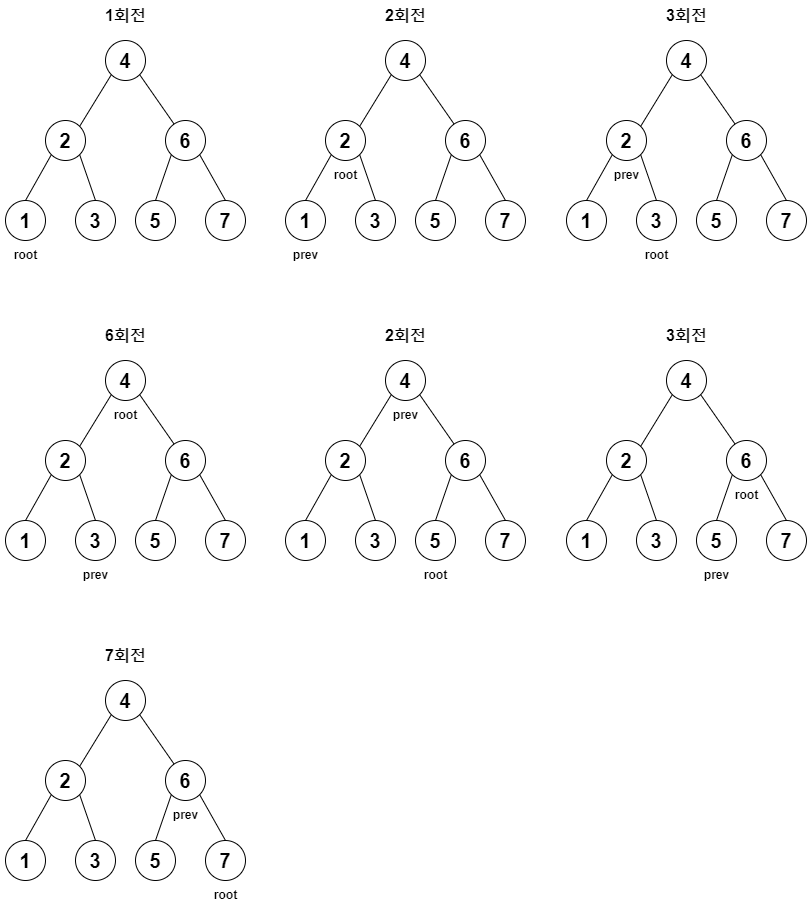
• 전체 while 반복문을 빠져나오면 해당 트리는 BST(이진 검색 트리)에 해당되므로, true를 반환하도록 한다.

  return true;